Rotations
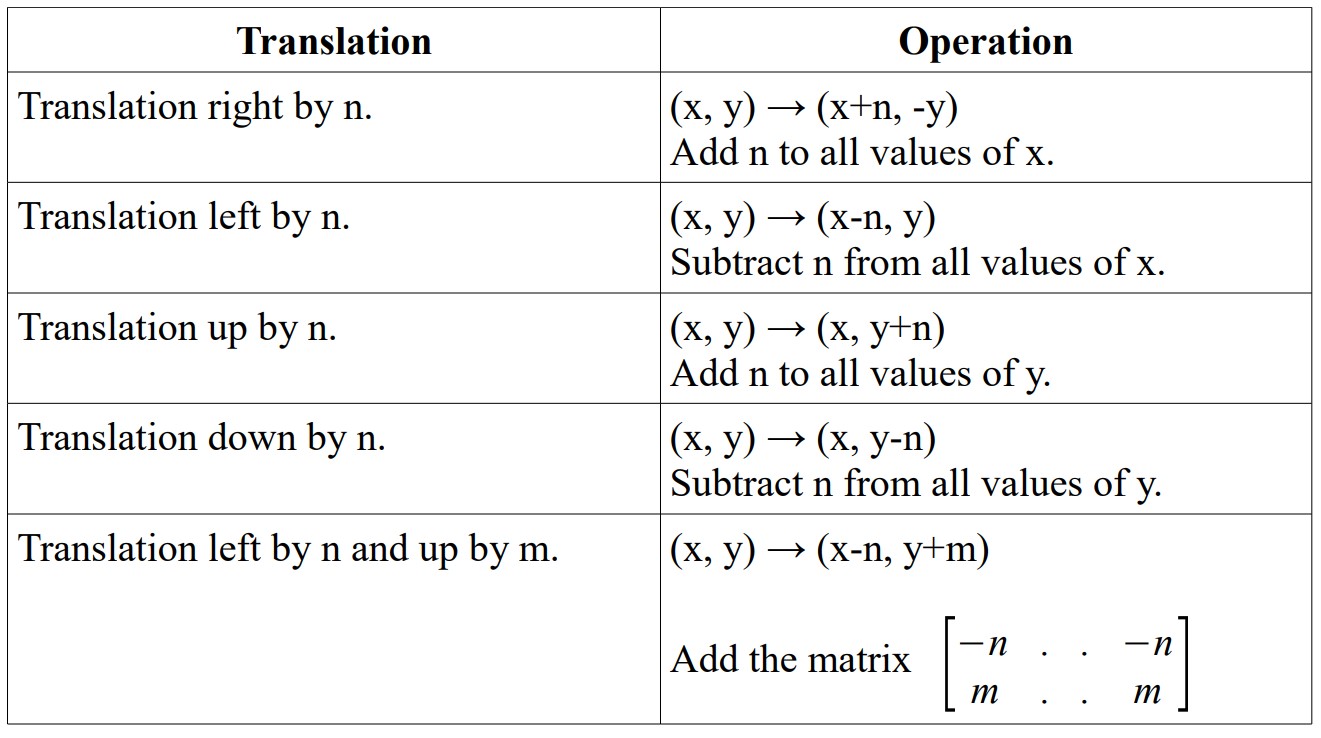
Translation of An Object
Note: A diagonal translation can be done by performing a left/right translation and an up/down translation simultaneously
Reflection of An Object About An Axis
Note: The meaning of ”reflection in x or y” is inconsistent in the texts. Make sure you know what your teacher means my this term.
Note: When multiplying matrices, order matters. The matrix below goes on the left and the coordinate matrix goes on the right. The number of columns in the left, reflection, matrix must match the number of rows in the right, coordinate, matrix.


Rotating An Object About The Origin

Rotating An Object About a Point Other Than The Origin
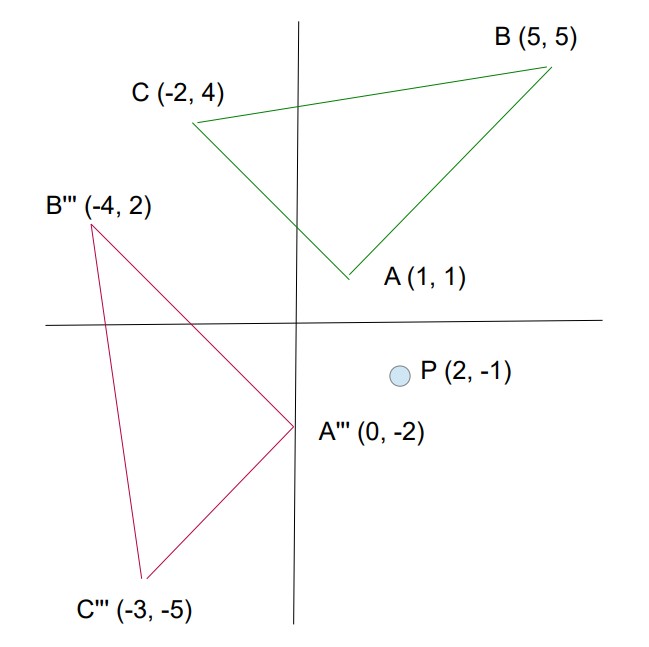
Example: We will rotate the triangle A(1,1), B(5,5), C(-2,4) 90 degrees counter-clockwise about the point P(2,-1)
- Step 1: Translate the triangle and the point of rotation 2 units (subtract 2 from every X) left and 1 unit up (add 1 to every Y) to place the point of rotation at the origin.
- A ( 1,1) --> A '(-1, 2)
- B ( 5,5) --> B' ( 3, 6)
- C (-2,4) --> C' (-4, 5)
- Step 2: Do the 90 degree counter-clockwise rotation using (X,Y) --> (-Y,X)
- A ( 1,1) --> A '(-1, 2) --> A'' (-2, -1)
- B ( 5,5) --> B' ( 3, 6) --> B'' (-6, 3)
- C (-2,4) --> C' (-4, 5) --> C'' (-5, -4)
- Step 3: Translate the new triangle in the direction opposite to Step 1, 2 units (add 2 to every X) right and 1 unit down (subtract 1 from every Y).
- A ( 1,1) --> A '(-1, 2) --> A'' (-2, -1) --> A''' ( 0, -2)
- B ( 5,5) --> B' ( 3, 6) --> B'' (-6, 3) --> B''' (-4, 2)
- C (-2,4) --> C' (-4, 5) --> C'' (-5, -4) --> C''' (-3, -5)