Rotations
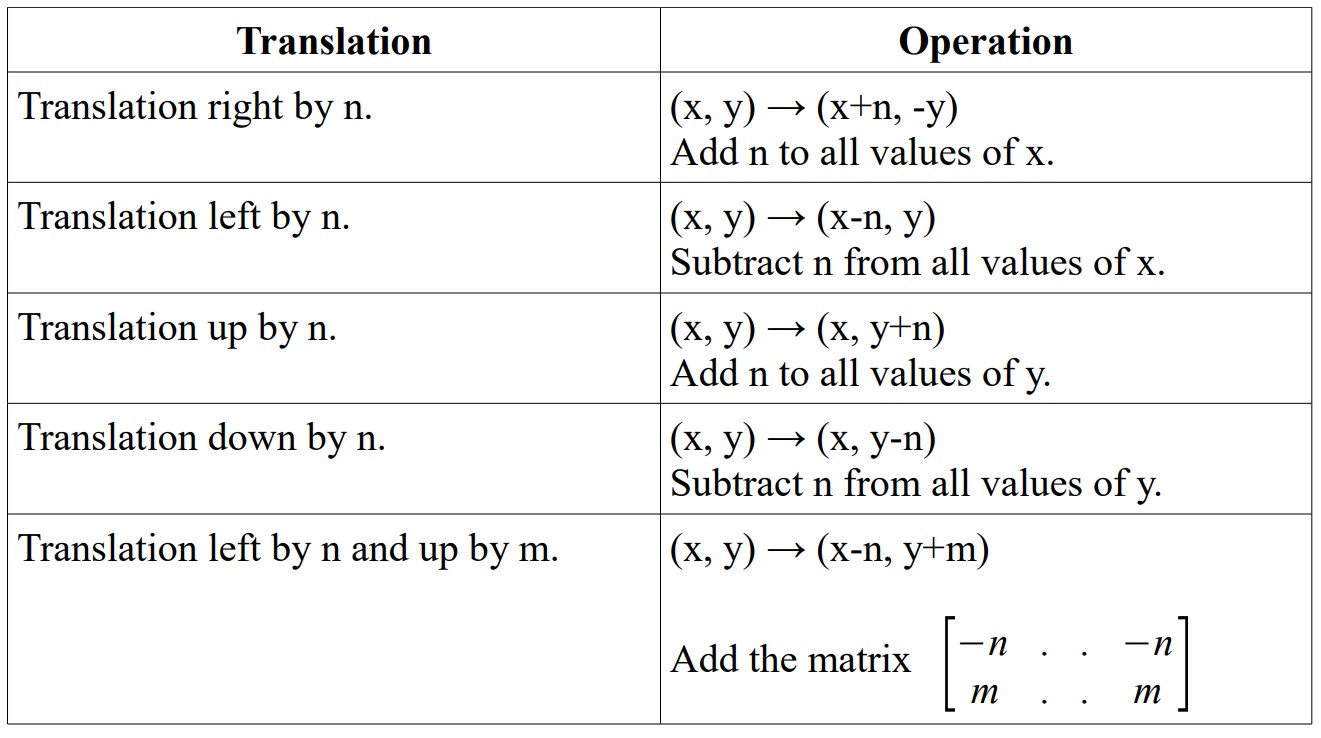
Translation of An Object
Note: A diagonal translation can be done by performing a left/right translation and an up/down translation simultaneously
Reflection of An Object About An Axis
Note: The meaning of ”reflection in x or y” is inconsistent in the texts. Make sure you know what your teacher means my this term.
Note: When multiplying matrices, order matters. The matrix below goes on the left and the coordinate matrix goes on the right. The number of columns in the left, reflection, matrix must match the number of rows in the right, coordinate, matrix.


Rotating An Object About The Origin

Rotating An Object About a Point Other Than The Origin
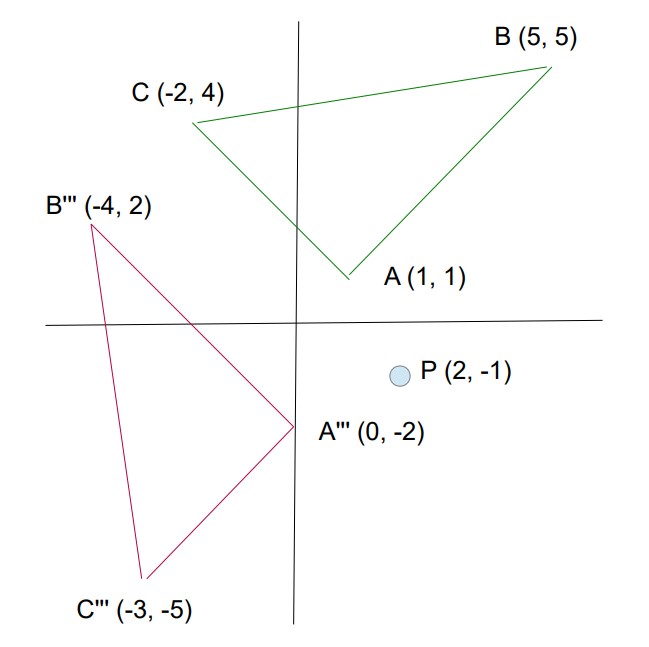
Example: We will rotate the triangle A(1,1), B(5,5), C(-2,4) 90 degrees counter-clockwise about the point P(2,-1)
- Step 1: Translate the triangle and the point of rotation 2 units (subtract 2 from every X) left and 1 unit up (add 1 to every Y) to place the point of rotation at the origin.
- A ( 1,1) --> A '(-1, 2)
- B ( 5,5) --> B' ( 3, 6)
- C (-2,4) --> C' (-4, 5)
- Step 2: Do the 90 degree counter-clockwise rotation using (X,Y) --> (-Y,X)
- A ( 1,1) --> A '(-1, 2) --> A'' (-2, -1)
- B ( 5,5) --> B' ( 3, 6) --> B'' (-6, 3)
- C (-2,4) --> C' (-4, 5) --> C'' (-5, -4)
- Step 3: Translate the new triangle in the direction opposite to Step 1, 2 units (add 2 to every X) right and 1 unit down (subtract 1 from every Y).
- A ( 1,1) --> A '(-1, 2) --> A'' (-2, -1) --> A''' ( 0, -2)
- B ( 5,5) --> B' ( 3, 6) --> B'' (-6, 3) --> B''' (-4, 2)
- C (-2,4) --> C' (-4, 5) --> C'' (-5, -4) --> C''' (-3, -5)


Very clear explanation of coordinate transformations. The logical sequence of translating, rotating, and translating back is presented in a simple and effective way, making complex rotation about an arbitrary point much easier to follow. This is a strong learning reference for anyone studying analytic geometry.
Well explained and mathematically precise. Emphasizing key concepts like matrix order, directional translation, and standard rotation rules helps build a solid conceptual foundation. The worked example provides practical clarity and reinforces understanding of geometric transformations.
Excellent presentation of transformation principles. Highlighting matrix order, coordinate translation, and rotation rules demonstrates strong mathematical clarity. Practical examples like rotating a triangle around a non-origin point greatly improve conceptual understanding and make the topic more accessible for learners.
Clear and well-structured explanation of geometric transformations. The step-by-step breakdown of translation, reflection, and rotation—especially rotation about a point other than the origin—makes the concept much easier to understand. This is a helpful guide for students learning coordinate geometry and matrix-based transformations.