Cryptography 101
In the article explaining Virtual Private Networks (VPNs), I intentionally did not discuss the cryptography employed by VPNs. Therefore, this companion article attempts to address that complicated subject, which consumed 30 years of my career. Since most web sites and VPNs generally use the Transport Layer Security (TLS) protocol, the information below is geared toward that protocol. See Transport Layer Security – Wikipedia, https://en.wikipedia.org/wiki/Transport_Layer_Security.
Disclaimer 1: This article does not cover the National Security Agency’s Type 1 High Assurance Internet Encryptor (HAIPE) products, described in High Assurance Internet Protocol Encryptor – Wikipedia, https://en.wikipedia.org/wiki/High_Assurance_Internet_Protocol_Encryptor. These products use a different protocol and classified algorithms, which are not discussed here.
Disclaimer 2: This article has nothing to do with Crypto Currency, although I will identify the algorithm (SHA-256) used by that financial technology.
Ethical, Legal, and Export Considerations
Cryptography, like many technologies, is amoral, that is, neither good nor bad. As such, it can be used for both good purposes and bad purposes, although it is now recognized that the good purposes far outweigh the bad purposes.
From WW-II to the late 1990s, the United States Government attempted to keep the technology out of the hands of terrorists, drug trafficers, etc.. Therefore, cryptography was the subject of strict export regulations under the International Traffic in Arms (ITAR) regulations by the Department of State (DoS) and Department of Commerce (DoC) as a weapon. Gradually, it was recognized that the restrictions were of little effect, because the bad guys could always procure the technology through other channels. It was also recognized that corporate security, personal security, e-commerce all depended on cryptography for good purposes. Today, the enforcement of the export regulations is more relaxed, as long as you use cryptography based on publicly published algorithms. However, you still have to go through the DoS or DoC.
Still, there are politicians that try to make a name for themselfs by trying to ban cryptography, with the claim that “child pornographers” use it. True, they do use it, but all of us also use it on a daily basis. Some countries and, occasionally, the United States attempt to either ban cryptography or force the use of government-provided cryptography to essentially spy on their populations.
Standards Bodies
It is always best to use cryptographic algorithms that have been thoroughly tested and evaluated, before being standardized. This is especially true for such industries as the Financial Services Industry, where they do not want to be held liable if the cryptography they use proves to not be sufficiently strong. While, most countries have standards bodies, many follow the lead of the United States for commercial algorithms.q
Internet Engineering Task Force (IETF)
This is an international standards body that sets the standards for all aspects of the Internet. They intentionally do not follow any countries lead and do their own thing, with a huge number of academic
experts from around the globe. All standards are developed over considerable time and with many iterations, by members of large working groups. The IETF’s documents are published as Request for Comments (rfx-xxxx), where rfcs are not updated bu replaced by new rfcs with new numbers.
National Institute of Standards and Technology (NIST), formerly National Bureau of Standards
This is United States standards body that sets the standards for many aspects of our lives. For cryptography, the NIST standards are used throughout the non-military parts of the United States Government and most commercial applications, including VPNs and the Financial Services Industry. NIST’s process for standardizing cryptography begins with a world-wide invitation to submit candidate algorithms and a world-wide invitation to evaluate and comment on algorithms. The process goes through several lengthy, democratic phases, and down-selects, until the final choice is made. The only part of the process that is not public, are evaluations and comments made to NIST by the National Security Agency. NIST’s final documents are published as Federal Information Processing Standard Publications (FIPS PUB xxx).
National Security Agency
The NSA is a closed environment that provides cryptographic algorithms and guidance for the United States military and related industries. Most of their output is classified and not openly available. The NSA also provides guidance for NIST and export determinations for DoS and DoC.
Classes of Cryptographic Algorithms
Digital Signature Algorithms
Digital signature is used by the TLS protocol to authenticate remote entities. For example, if you see :https” (S = secure) and a padlock in you browser, the entity, usually a web site, to which you are connected has been successfully authenticated.
There are two approaches to digital signatures:
For short messages, the message is encrypted by the signer’s private key and decrypted by the recipient with the signer’s public key. This is called digital signature with message recovery or “sigcryption.” It works only with the RSA algorithm and not with DSA or ECDSA.
For longer messages, a hash of the message is generated, as described below, and it is this hash that is signed with the signer’s private key. The recipient generates a hash of the received message and decrypts thes igned hash with the signer’s public key. If the two hashes match, the message is authenticated. This is called “digital signature with appendix” and is not used by the TLS protocol.
The RSA algorithm is based on the fact that multiplication of two large prime numbers is easy, while factoring a large composite number into its constituent prime numbers is computationally infeasible. By “large” we currently use 4,096-bit or around 1,200 decimal digit composite numbers.
The DSA and ECDSA algorithms are based on the same finite field and elliptic curve mathematics as the key agreement algorithms, described below.
The TLS protocol typically uses the RSA digital signature algorithm, with appendix, to validate signed certificates for remote entity authentication. The RSA algorithm is best for this application, because the slow signing operation is done only once, which the much faster verification operation is done very frequently on smaller computers.
See:
RSA cryptosystem – Wikipedia, https://en.wikipedia.org/wiki/RSA_cryptosystem NIST FIBS PUB 186, the Digital Signature Standardized and Elliptic Curve Digital Signature Standard

Notes:
The signing process involves creating a hash of the
message, signing/encrypting the hash and
appending it to the plaintext message.
The plaintext message and signed hash are sent to
the recipient.
The verification process involves creating a hash of
the received message, decrypting the received hash
created by the signer, and comparing the two
hashes. If the hashes match, the message is
authentic and unaltered.
Digital Signature with Appendix
Asymmetric Key Transport Algorithms
This subject applies only to the RSA algorithm, based on the integer factorization problem (IFP) and described above, and not the DSA or ECDSA algorithms.
For key transport, one entity, such as your browser or VPN randomly generates a key for the symmetric key bulk data encryption algorithm. This key then needs to be securely transmitted to the remote entity, usually a website or VPN host. To do this, the random key is RSA encrypted using the remote entity’s public key, recovered in the authentication process. The encrypted symmetric key is then sent to the remote entity, which is the only entity that can decrypt it, because only it has the private key, corresponding to the public key used to encrypt the symmetric key.
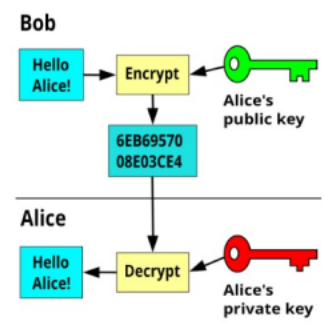
Notes:
A message or secret key, shorter than the RSA
modulus, is encrypted by the sender, using the
recipient’s public key.
The transmitted message can only be decrypted by
the recipient, as only the recipient possesses the
private key.
If the decrypted message/key makes sense, both the
sender and recipient now share the same
message/key.
Any error will cause the decrypted value to be
nonsense.
Asymmetric Key Agreement Algorithms
Asymmetric key agreement algorithms allow two communicants to “communicate in public” and “compute in private” to generate a shared secret, which is then used as the key for a symmetric key encryption algorithm. With these algorithms, each communicate generates a random private key, and, from that key, generates a public key, using a one-way mathematical function. They then each share the public keys with the other communicant and perform a second computation with their private keys to generate the shard secret.
The foundational algorithm of this type is the Diffie-Hellman algorithm, basedon the discreet log problem (DLP). See Diffie–Hellman key exchange – Wikipedia, https://en.wikipedia.org/wiki/Diffie Hellman_key_exchange. There are variants of this algorithm, such as the Elliptic Curve Diffie-Hellman algorithm, which uses different underlying mathematics based on the elliptic curve discreet log problem (ECDLP). The MQV (Menezes–Qu–Vanstone) and ECMQV algorithms perform the same key agreement function, plus remote entity authentication.
These algorithms are all based on the fact that exponentiation in the finite field and point multiplication on an elliptic curve is easy, while the reverse operation is computationally infeasible.
The TLS protocol frequently uses Diffie-Hellman to establish an unauthenticated secure channel between communicates, through which entity authentication and key exchanged is subsequently performed.
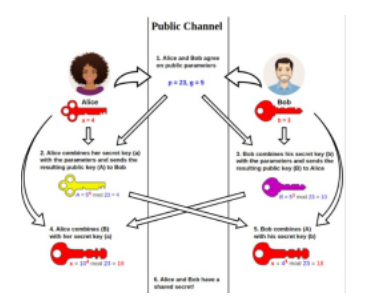
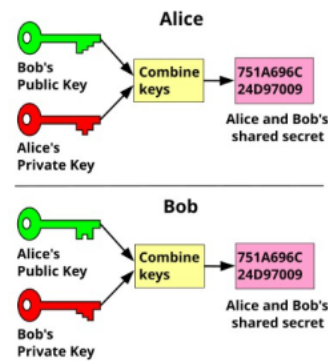
Difffie-Hellman Key Agreaement Protocol
Symmetric Key Bulk Encryption Algorithms
Non-mathematical symmetric key encryption algorithms are used to encrypt the actual data for secure communications. They are symmetric key, with both communicants requiring possession of the same key for both encryption and decryption. While there are many, many symmetric key algorithms, the most common algorithm used today is the NIST Advanced Encryption Standard with a 256-bit key (AES-256).
The current standards are:
NIST FIPS PUB 197, the Advanced Encryption Standard (AES)
NIST SP 800-38, Modes of Operation
See Cryptographic Standards and Guidelines | CSRC,
https://csrc.nist.gov/projects/cryptographic-standards-and-guidelines
Secure Hash (Message Digest) Algorithms
A secure hash algorithm takes a message of arbitrary length and reduces it to a fixed-length value that is dependent upon all bits in the message. The resulting hash is large enough, 224 to 512 bits, that it is computationally infeasible to generate a different message or modification of the original message that
results in the same hash. These hashes are often encrypted by a digital signature algorithm, providing what is knows as “digital signature with appendix,” the plaintext message with the signature appended.
SHA-256 is typically used in the crypto currency technology and will be under threat by quantum computing. This poses a major problem for crypto currency and its mining operations.
The current standards are:
NIST FIBS PUB 180-4, the SHA-2 Secure Hash Standard
NIST FIBS PUB 202, SHA-3 Standard (quantum resistant)
IETF rfc-6234
Algorithm Suites and the TLS Protocol
Given the number of algorithm types and number of algorithms in each type, this is the “ethnic menu” problem on steroids. The solution is to define the equivalent of the “combination Plate” that makes sense. These combinations are called algorithm suites and are each defined by a unique number, called an Object Identifier (OID). This allows new suites to be defined and less secure suites to be phased out over time. By sharing and comparing OIDs, two communicants can determine the best, common algorithm suite to be used in each communication.
The TLS protocol is very versatile, but I will only describe the use in this context. Here are the steps in the TLS Handshake.
ClientHello: The client sends a message specifying the highest TLS protocol version it supports, a random number, and a prioritized list of supported cipher suites.
ServerHello: The server responds with a message containing the chosen protocol version, a random number, and the selected cipher suite.
Server Certificate: The server sends its signed digital certificate to the client for authentication.
Key Exchange: The client and server exchange cryptographic parameters to generate a shared secret key via a key agreement algorithm or to send a secret key from client to server via a key transport algorithm.
ChangeCipherSpec: Both parties send a message indicating that subsequent messages will be encrypted using the selected bulk encryption algorithm and shared secret key.
Finished: Both parties send a message to verify that the handshake was successful The TLS protocol is very flexible and contains mechanisms to provide:
Integrity: Protection again message modification by a man-in-the-middle.
Forward and Backward Security: If a shared secret key is compromized, an attacker can not decrypt traffic sent between the same communicants in either a previous or a future TLS session.
Related Questions and Answers
Is the RSA Algorithm Broken?
key (a large integer) that has been factored into its two constituent prime numbers. This does not make it any easier to factor another key. A quantum computer recently factored a 22-bit number, which is significant, but trivial. The largest number factored to date was 829 bits, factored in 2020. See RSA Factoring Challenge – Wikipedia, https://en.wikipedia.org/wiki/RSA_Factoring_Challenge. Factoring such a number typically takes around 2,000 cpu-years, which might be 1,000 computers dedicated to this task for 2 years. Currently, we use 4096-bit keys, with some 2048-bit keys still being around. Since each increment of 6 bits in key length doubles the factoring effort, we are still far from factoring currently used keys. Quantum computing may change that in the future.
Can the NSA Break Our Cryptography?
Maybe and maybe not. If the NSA can break our cryptography, it would be in the interest of national security to not make that known. If the NSA can not break our cryptography, it would also be in the interest of national security to not make that known either. Suffice it to say that the NSA knows everything academia knows, but academia does not know what else the NSA might know. The NSA also has an army of mathematicians and an enormous amount of computational power.
What is Quantum Resistant Cryptography?
If quantum computing comes to maturity, it will have a giant leap in computational power, compared to today’s computers. This means that all traditional cryptographic algorithms will become weak and subject to attack. Therefore, there has been a decade-plus long effort by all standards bodies to develop new cryptographic algorithms that can withstand attack by the quantum computers of the future.
What is End-to-End Encryption?
For example, if I am exchanging emails or files with another party, the data is fully encrypted between my platform and the other party’s platform, without the ability of a third party, such as an email provider, to decrypt the communications.
By contrast, my wife was in health care and had a device to provided encrypted messaging for medical data, protected under the Health Insurance Portability and Accountability Act (HIPAA). The data was encrypted between one mobile device and the provider, decrypted by the provider, and then re encrypted for transfer to the recipient’s mobile device. This is an example that is not end-to-end encryption.
In multi-party communications, such as a conference call, end-to-end encryption is essentially difficult or impossible, because multiple “ends” of a connection exist. Here, you need a trusted intermediary provider, such as described in the previous paragraph. That provider could be one of the communicants, with a platform power enough to process encryption of data to and from each of the other communicants.
Role of Elliptic Curve Cryptography
Any algorithm based on the discreet log problem (DLP), such as Diffie-Hellman and the Digital Signature Algorithm (DSA) can also be based on the elliptic curve discreet log problem (ECDLP). The advantage of ECDLP based algorithms is that they are fully exponential, meaning that the difficulty of cracking a key doubles for each additional bit of field length. By contrast, DLP based algorithms are sub-exponential, with the difficulty of cracking a key doubling for each six additional bits of field length. This means that ECDLP offers much greater security for much shorter field lengths, but at the expense of much more complicated mathematics.
Note there is no elliptic curve equivalent for algorithms based on the integer factorization problem (IFP), such as RSA.
Role of Entropy and Randomness
Cryptography relies heavily upon the ability to generate good, cryptographically strong random numbers. Compared to just statistically strong, cryptographically strong implies that, given knowledge on one number, it is impossible to determine the previous or next random number generated. This is often the “Achilles’ heel” of cryptographic implementations, especially on platforms such as personal computers. NIST has several Special Publications offering guidance for random and pseudo-random (deterministic) number generators; SP 800-90A, 800-90B, and 800-90C.

