Financial formulae
Financial Calculation Formulae
Continuously compounded interest on a fixed investment
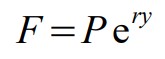
F = Future value
P = Initial principle invested
r = Annual percentage interest rate, APR
y = Number of years invested
e = Euler’s number, 2.71828…, the base of the natural logarithm
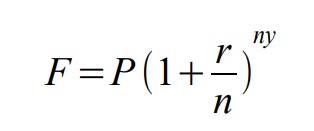
F = Future value
P = Initial principle invested
r = Annual percentage interest rate, APR
n = Number of times compounded per year
y = Number of years invested
r/n = Interest rate per compounding period
ny = Number of times compounded over y years

y = the number of years required to achieve a financial goal are interest rate r
ny = the number of compoundings to achieve a financial goal are interest rate r
You must round up to the next compounding to fully achieve the financial goal.
Any base log can be used, as long as you are consistent.

where: r = the interest rate required to achieve a financial goal in y years.
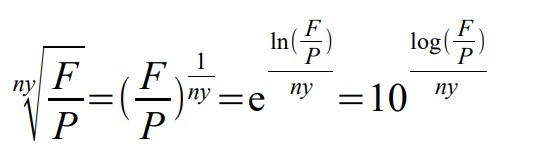
If your calculator does not have and y √ x function, logs may be used as shown above. (Any base log can be used, as long as the log and base are consistent.)
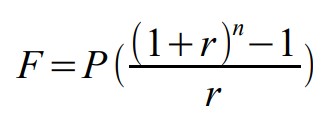
F = Future value
P = Additional principle invested every compounding period
r = Interest rate per compounding period
n = Number of times compounded
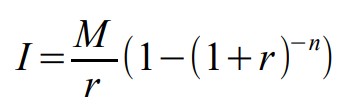
I = Initial investment required to receive n payments of M dollars
(a loan made to the bank)
M = Amount of money received from the annuity per period
r = Interest rate per compounding period
n = Number of payments received and times compounded

M = The periodic payments to be made
L = Initial principle of loan taken
r = Interest rate per payment and compounding period
n = Number of payments to be made
Mn = Total cost of borrowing L dollars over n payments
B = Balance due after making n payments of M dollars
I = Total interest paid on borrowing L dollars over n payments
n = Number of payments of M dollars to pay off a loan of L dollars at rate r
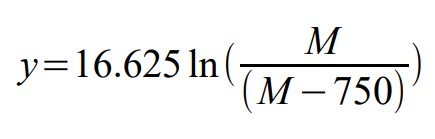
What does capitalization of a loan mean?
Example:
- As a college student, you take out a college loan that has a non-zero interest rate, but payments need to be made for 5 years. You are deferring payment of both the initial loan and the interest.
- Every month for those 5 years, you effectively borrow more money from the lender to pay the interest on the loan and accrued interest.
- At the end of the 5 years, you now have a larger loan, which you must now pay as a conventional mortgage.
Note:
- Part 1, the first 5 years: This is treated as a saving account computation, where the initial value is the loan amount. The final value is the initial loan plus accrued interest.
- Part 2, the payoff years: This is treated as a conventional mortgage computation, where the loan amount is the initial loan plus the accrued interest.

